Master the Pyramid Volume Formula: Easy Guide to Perfect Calculations 2026

Introduction
Have you ever looked at the Great Pyramid of Giza and wondered how much space exists inside? Or perhaps you’re working on a math problem and feeling stuck on calculating pyramid volumes? You’re not alone. The pyramid volume formula is one of those mathematical concepts that sounds complicated but becomes surprisingly simple once you understand the logic behind it.
Understanding how to calculate the volume of a pyramid opens doors to solving practical problems in architecture, engineering, and everyday situations. Whether you’re a student tackling geometry homework, a professional working on design projects, or simply someone curious about mathematics, mastering this formula will serve you well. In this comprehensive guide, I’ll walk you through everything you need to know about the pyramid volume formula, from basic concepts to advanced applications.
What Is a Pyramid and Why Does Volume Matter?
A pyramid is a three-dimensional geometric shape with a polygonal base and triangular faces that meet at a single point called the apex or vertex. You can find pyramids everywhere, from ancient Egyptian monuments to modern architectural designs and even the humble roof of many buildings.
Calculating volume matters because it tells you how much space exists inside a three-dimensional object. When architects design buildings, they need accurate volume calculations. When manufacturers create pyramid-shaped packaging, they must know the capacity. When students solve geometry problems, understanding volume helps them grasp spatial relationships.
The beauty of the pyramid volume formula lies in its simplicity. Unlike some mathematical concepts that require complex calculations, this formula uses straightforward multiplication and division. Once you learn it, you’ll recognize patterns that make calculations almost intuitive.
The Basic Pyramid Volume Formula Explained
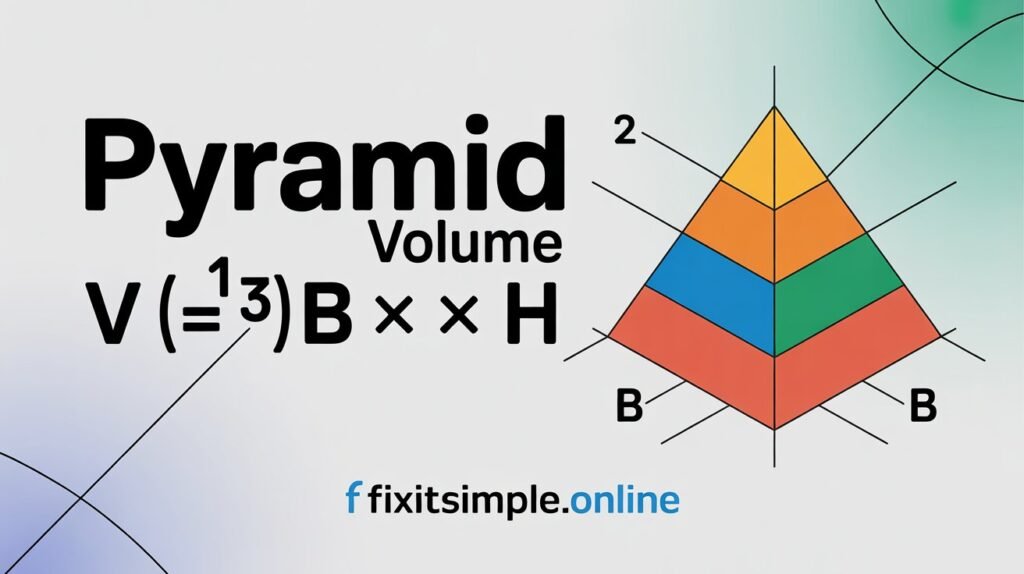
The pyramid volume formula is remarkably elegant. Here it is: V = (1/3) × B × h
Let me break down what each part means. V represents the volume you’re trying to find. B stands for the area of the base, which can be any polygon. The letter h represents the perpendicular height from the base to the apex.
The fraction one-third is the key element that distinguishes pyramids from prisms. A pyramid always has exactly one-third the volume of a prism with the same base area and height. This relationship isn’t arbitrary. It comes from integral calculus, though you don’t need to understand calculus to use the formula effectively.
Think of it this way: if you filled three identical pyramids with water and poured them into a prism with the same base and height, you’d fill that prism perfectly. This visual helps many people remember why we multiply by one-third.
Understanding the Components of the Formula
Base Area Calculation
The base of your pyramid determines which formula you’ll use to find B. Different base shapes require different area calculations, but the pyramid volume formula itself stays the same.
For a square pyramid, you multiply the side length by itself. If each side measures 6 meters, the base area equals 36 square meters. For a rectangular pyramid, you multiply length times width. A triangle-based pyramid requires you to use one-half times base times height for the triangular base area.
Regular hexagonal pyramids, pentagonal pyramids, and other polygonal bases each have their own area formulas. The important thing to remember is that you must calculate the base area correctly before applying the pyramid volume formula. Many calculation errors happen at this step, not in the volume formula itself.
Height Measurement
Height in the pyramid volume formula always means the perpendicular distance from the base to the apex. This point trips up many learners because they confuse it with the slant height, which is the distance along the pyramid’s face from the base edge to the apex.
Imagine dropping a line straight down from the apex to the base. Where it touches the base should form a 90-degree angle. That distance is your height. In a right pyramid, where the apex sits directly above the center of the base, measuring height is straightforward. In oblique pyramids, where the apex leans to one side, you need to be more careful.
Sometimes you’ll need to use the Pythagorean theorem to find the height when you only know the slant height and base dimensions. This adds an extra step but follows logical mathematical principles you probably already know.
Step-by-Step Guide to Using the Pyramid Volume Formula
Let me walk you through a complete calculation from start to finish. This methodical approach will help you avoid mistakes and build confidence.
Step 1: Identify the Base Shape Look at your pyramid and determine what polygon forms the base. Is it a square, rectangle, triangle, or another shape? Write this down.
Step 2: Calculate Base Area Use the appropriate formula for your base shape. Double-check your arithmetic here because errors multiply through the rest of the calculation.
Step 3: Measure or Find the Height Locate the perpendicular height. Make sure you’re not using slant height by mistake. If you need to calculate height from other measurements, do that now.
Step 4: Apply the Pyramid Volume Formula Multiply the base area by the height. Then multiply that result by one-third. Alternatively, you can divide by three, which gives the same answer.
Step 5: Check Your Units Volume always uses cubic units. If your measurements were in meters, your answer should be in cubic meters. If in centimeters, use cubic centimeters.
Practical Examples with Real Numbers
Let’s work through several examples to make this concrete. I find that seeing multiple scenarios helps the concept stick.
Example 1: Square Pyramid Imagine a pyramid with a square base where each side measures 10 feet. The height is 12 feet. First, calculate the base area: 10 × 10 = 100 square feet. Now apply the formula: V = (1/3) × 100 × 12 = 400 cubic feet.
Example 2: Rectangular Pyramid Consider a pyramid with a rectangular base measuring 8 meters by 6 meters. The height is 9 meters. Base area equals 8 × 6 = 48 square meters. Volume equals (1/3) × 48 × 9 = 144 cubic meters.
Example 3: Triangular Pyramid Picture a pyramid with a triangular base. The triangle has a base of 5 inches and a height of 4 inches. The pyramid’s height is 7 inches. Triangle area equals (1/2) × 5 × 4 = 10 square inches. Pyramid volume equals (1/3) × 10 × 7 = 23.33 cubic inches.
Common Mistakes to Avoid
Through years of teaching and learning, I’ve noticed several errors that people make repeatedly when using the pyramid volume formula. Awareness helps you avoid them.
Confusing Slant Height with Perpendicular Height This is the number one mistake. Always verify that you’re using the vertical height, not the measurement along the face of the pyramid. Draw a diagram if necessary to clarify which measurement you have.
Forgetting the One-Third Factor Some people calculate base area times height and forget to multiply by one-third. This gives them a volume three times too large. The answer looks reasonable, so they don’t catch the error. Always double-check that you’ve included this crucial fraction.
Miscalculating Base Area Each base shape has its own area formula. Make sure you’re using the right one. A common error is calculating the perimeter instead of the area, or mixing up which dimensions to multiply.
Unit Conversion Errors If your base uses meters and your height uses centimeters, you must convert to the same unit before calculating. The final answer should be in cubic units that match your chosen measurement system.
Rounding Too Early When you round intermediate calculations too aggressively, errors accumulate. Keep extra decimal places during calculations and round only your final answer to the appropriate precision.
Applications in Real Life
The pyramid volume formula isn’t just an abstract mathematical exercise. It has genuine practical applications that affect real-world decisions and designs.
Architects use this formula when designing buildings with pyramid-shaped features. They need accurate volume calculations to estimate materials, understand weight distribution, and plan interior spaces. A small error in volume calculation can lead to significant problems in construction.
Engineers apply the pyramid volume formula in various fields. Civil engineers might calculate the volume of pyramid-shaped structures or earthworks. Chemical engineers might design pyramid-shaped containers for specific storage needs. The formula helps them optimize designs for efficiency and functionality.
Manufacturing companies use volume calculations for packaging design. Pyramid-shaped boxes need accurate volume measurements to ensure they hold the right amount of product while minimizing wasted space and material costs.
Even in art and sculpture, understanding pyramid volumes helps creators work with three-dimensional forms. When you know how much space a pyramid occupies, you can better plan compositions and material requirements.
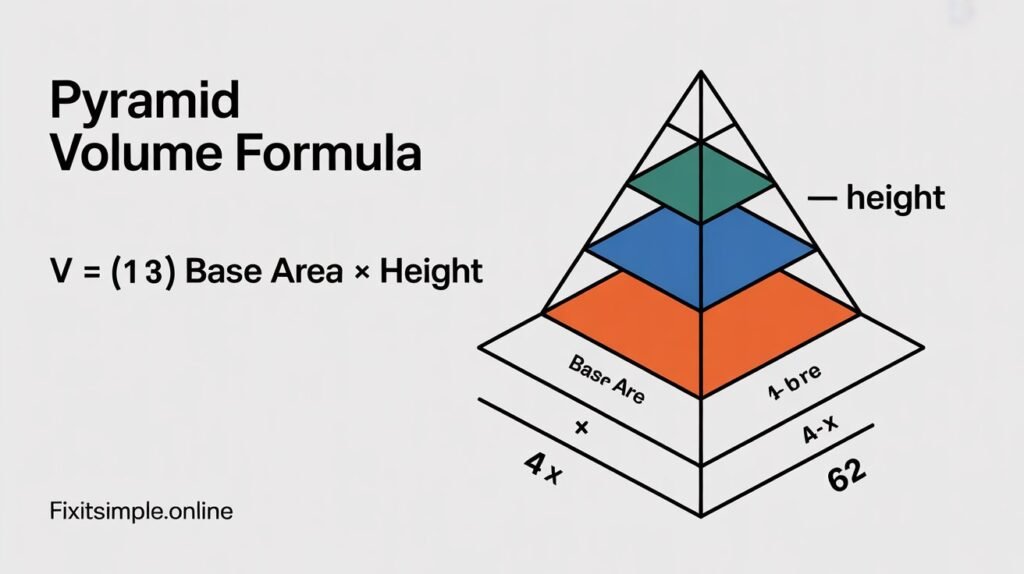
Advanced Considerations and Variations
Once you’ve mastered the basic pyramid volume formula, you can explore more complex scenarios that build on this foundation.
Truncated Pyramids A truncated pyramid, also called a frustum, has its top portion cut off parallel to the base. Calculating this volume requires a different formula that accounts for both the bottom base and the top base. The formula is: V = (h/3) × (B₁ + B₂ + √(B₁ × B₂)), where B₁ and B₂ are the two base areas.
Composite Shapes Sometimes you’ll encounter shapes made of multiple pyramids or pyramids combined with other geometric forms. You can calculate the total volume by finding each component’s volume separately and adding them together. This technique applies the pyramid volume formula multiple times within a single problem.
Pyramids with Irregular Bases Not all pyramids have neat, regular polygons as bases. For irregular polygonal bases, you might need to divide the base into triangles, calculate each triangle’s area, sum them for the total base area, and then apply the standard pyramid volume formula.
Tips for Remembering the Formula
Memory techniques can help you recall the pyramid volume formula whenever you need it, even without a reference sheet handy.
The One-Third Connection Remember that a pyramid always has one-third the volume of a prism with the same base and height. If you forget the exact formula, reconstructing it from this principle works perfectly.
Visual Mnemonics Picture three pyramids stacked to fill a box. This image reinforces the one-third relationship and helps you remember why that fraction appears in the formula.
Practice Regularly The more you use the pyramid volume formula, the more automatic it becomes. Work through practice problems regularly, even just a few each week, to keep the concept fresh in your mind.
Teach Someone Else Explaining the pyramid volume formula to another person forces you to organize your understanding clearly. This process strengthens your own grasp of the concept and reveals any gaps in your knowledge.
Comparing Pyramid Volume to Other 3D Shapes
Understanding how pyramid volume relates to other three-dimensional shapes deepens your geometric intuition and provides helpful reference points.
A cone is essentially a pyramid with a circular base. The formula is nearly identical: V = (1/3) × πr² × h. The one-third factor appears here too, connecting cones and pyramids mathematically.
A prism has three times the volume of a pyramid with the same base and height. This relationship is fundamental and helps you estimate and check your work. If you accidentally calculate a pyramid volume that equals or exceeds a corresponding prism, you know something went wrong.
A sphere’s volume formula differs completely: V = (4/3) × πr³. However, understanding multiple volume formulas together helps you choose the right one for each shape and recognize the unique mathematical properties of different forms.
Solving for Unknown Variables
Sometimes you’ll know the volume and need to find the height or base dimensions. The pyramid volume formula works backward just as well as forward.
Finding Height When Volume and Base Are Known Rearrange the formula to h = 3V/B. Multiply the volume by three, then divide by the base area. This gives you the perpendicular height.
Finding Base Area When Volume and Height Are Known Rearrange to B = 3V/h. Multiply the volume by three and divide by the height to get the base area.
Finding Base Dimensions for Regular Pyramids If you know the base is square and you’ve calculated the base area, take the square root to find the side length. For rectangular bases, you’ll need additional information to find both dimensions.
These reverse calculations appear in optimization problems, design challenges, and theoretical mathematics. Being comfortable working the formula in all directions makes you more versatile in problem-solving.
Technology and Calculation Tools
While understanding the pyramid volume formula conceptually is essential, modern tools can speed up calculations and reduce arithmetic errors.
Scientific calculators have all the functions you need for pyramid volume calculations. Make sure you know how your calculator handles fractions and order of operations to avoid input errors.
Online calculators specifically designed for pyramid volume can verify your hand calculations. Input your measurements and compare the result to what you calculated manually. Discrepancies help you identify and correct mistakes.
Spreadsheet programs like Excel or Google Sheets can automate pyramid volume calculations, especially useful when you need to calculate volumes for many pyramids with different dimensions. Set up the formula once, then change the input values as needed.
Computer-aided design software includes volume calculation features for complex three-dimensional models. These professional tools apply the pyramid volume formula automatically as part of larger design workflows.
Teaching Pyramid Volume to Others
If you’re helping someone else learn the pyramid volume formula, certain approaches work better than others based on my experience with students and peers.
Start with concrete examples using real objects. Measure actual pyramid-shaped items and calculate their volumes together. This tangible approach makes abstract formulas feel more relevant and understandable.
Use visual aids extensively. Draw diagrams showing the base, height, and how they relate to the formula. Color-code different components to help learners track which measurement corresponds to which variable.
Build from simpler concepts. Make sure the person understands area before tackling volume. Confirm they can calculate base areas for different polygons before introducing the one-third factor and height dimension.
Encourage estimation before calculation. Ask “Will this volume be larger or smaller than that one?” Developing intuition for relative sizes helps learners catch major errors and builds confidence in their understanding.
Historical Context and Mathematical Development
The pyramid volume formula has ancient roots that connect modern mathematics to civilizations thousands of years old. Understanding this history adds richness to your knowledge.
Ancient Egyptian mathematicians worked with pyramid volumes while constructing their famous monuments. The Moscow Mathematical Papyrus, dating to around 1850 BCE, contains a correct formula for truncated pyramid volume, showing sophisticated mathematical understanding.
Greek mathematicians, particularly Archimedes and Euclid, rigorously proved relationships between pyramid and prism volumes using geometric arguments. Their work established the mathematical foundation we still use today.
The development of calculus in the 17th century provided new tools for understanding why the one-third relationship exists. Integral calculus allows us to derive the pyramid volume formula from first principles, though the formula itself predates calculus by millennia.
Conclusion
Mastering the pyramid volume formula gives you a powerful tool for understanding three-dimensional space and solving practical problems. The formula V = (1/3) × B × h might seem simple, but its applications span architecture, engineering, manufacturing, and pure mathematics.
You now know how to identify base shapes, calculate their areas, measure perpendicular height correctly, and apply the formula step by step. You’ve seen real examples, learned common mistakes to avoid, and explored both basic and advanced applications. This knowledge serves you whether you’re completing homework assignments, designing structures, or simply satisfying your curiosity about how the world works.
Remember that practice builds confidence and competence. Work through problems regularly, check your answers, and don’t hesitate to revisit the concepts when you need a refresher. The pyramid volume formula becomes second nature with consistent use.
What pyramid volume calculation will you tackle first? Will you measure objects around your home, help someone with their math homework, or apply this knowledge to a professional project?
Frequently Asked Questions
What is the pyramid volume formula? The pyramid volume formula is V = (1/3) × B × h, where V represents volume, B represents the area of the base, and h represents the perpendicular height from the base to the apex. This formula works for any pyramid regardless of its base shape.
Why do we multiply by one-third in the pyramid volume formula? A pyramid has exactly one-third the volume of a prism with the same base area and height. This mathematical relationship comes from the geometric properties of these shapes and can be proven using integral calculus or geometric decomposition methods.
How do I find the height of a pyramid for volume calculations? Measure the perpendicular distance from the base to the apex. This is different from slant height, which runs along the pyramid’s face. If only slant height and base dimensions are known, use the Pythagorean theorem to calculate the perpendicular height.
Can the pyramid volume formula work for any base shape? Yes, the pyramid volume formula works for pyramids with any polygonal base, including triangular, square, rectangular, pentagonal, hexagonal, and irregular polygon bases. You simply need to calculate the base area using the appropriate formula for that specific polygon.
What’s the difference between a pyramid and a cone in volume calculation? A cone is essentially a pyramid with a circular base. The formulas are structurally identical, both using one-third times base area times height. For cones, you use πr² for the base area instead of a polygonal area calculation.
What units should I use for pyramid volume? Volume is always expressed in cubic units. If your measurements are in meters, the volume is in cubic meters. If in feet, use cubic feet. If in centimeters, use cubic centimeters. Always ensure all measurements use the same unit before calculating.
How do I calculate the volume of a truncated pyramid? A truncated pyramid uses a different formula: V = (h/3) × (B₁ + B₂ + √(B₁ × B₂)), where h is the height, B₁ is the area of the larger base, and B₂ is the area of the smaller top base. This accounts for both parallel bases.
What are common mistakes when using the pyramid volume formula? The most frequent errors include confusing slant height with perpendicular height, forgetting to multiply by one-third, miscalculating the base area, using inconsistent units, and rounding intermediate calculations too aggressively.
Can I use the pyramid volume formula to find base area or height? Yes, you can rearrange the formula. To find height when volume and base are known, use h = 3V/B. To find base area when volume and height are known, use B = 3V/h. This flexibility makes the formula useful for various problem types.
How accurate do my measurements need to be for pyramid volume calculations? Accuracy requirements depend on your application. For academic exercises, follow the precision indicated in the problem. For practical applications like construction or manufacturing, consider the acceptable margin of error for your specific project and measure accordingly.
Also read fixitsimple.online